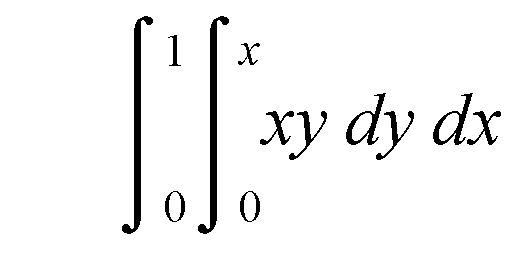Downward closures

The requirements for Ada 83, (Strawman .. Steelman) were strangely silent about whether parameters of subprograms could themselves be subprograms as was the case in Algol 60 and Pascal. Remember that Pascal was one of the languages on which the designs for the DoD language were to be based.

The predictability aspects of the requirements were interpreted as implying that all subprogram calls should be identified at compilation time on the grounds that if you didn't know what was being called than you couldn't know what the program was going to do. This was a particularly stupid attitude to take. The question of predictability (presumably in some safety or security context) really concerns the behaviour of particular programs rather than the universe of all programs that can be constructed in a language.

In any event the totality of subprograms that might be called in a program is finite and closed. It simply consists of the subprograms in the program. Languages such as Ada are not able to construct totally new subprograms out of lesser components in the way that they can create say floating point values.

So the world had to use generics for many applications that were natural for subprograms as parameters of other subprograms. Thankfully many implementers avoided the explosion that might occur with generics by clever code sharing which in a sense hid the parameterization behind the scenes.

The types of applications for which subprograms are natural as parameters are any where one subroutine is parameterized by another. They include many mathematical applications such as integration and maximization and more logical applications such as sorting and searching and iterating.

As outlined in the Introduction, the matter was partly improved in Ada 95 by the introduction of named access-to-subprogram types. This was essentially done to allow program call back to be implemented.

Program call back is when one program passes the "address" of a subprogram within it to another program so that this other program can later respond by calling back to the first program using the subprogram address supplied. This is often used for communication between an Ada application program and some other software such as an operating system which might even be written in another language such as C.

Named access to subprogram types certainly work for call back (especially with languages such as C that do not have nested subprograms) but the accessibility rules which followed those for general access to object types were restrictive. For example, suppose we have a general library level function for integration using a named access to subprogram type to pass the function to be integrated thus

then we cannot even do the simplest integration of our own function in a natural way. For example, suppose we wish to integrate a function such as Exp(X**2). We can try

But this is illegal because of the accessibility check necessary to prevent us from writing something like

Evil: Integrand;
X: Float;
...
declare
   Y: Float;
   function F(X: Float) return Float is
      ...
      Y := X;    --assign to Y in local block
      ...
   end F;
begin
   Evil := F'Access:    -- illegal
end;
   X := Evil(X);    -- call function out of context

Here we have attempted to assign an access to the local function F in the global variable Evil. If this assignment had been permitted then the call of Evil would indirectly have called the function F when the context in which F was declared no longer existed; F would then have attempted to assign to the variable Y which no longer existed and whose storage space might now be used for something else. We can summarise this perhaps by saying that we are attempting to call F when it no longer exists.

Ada 2005 overcomes the problem by introducing anonymous access to subprogram types. This was actually considered during the design of Ada 95 but it was not done at the time for two main reasons. Firstly, the implementation problems for those who were using display vectors rather than static links were considered a hurdle. And secondly, a crafty technique was available using the newly introduced tagged types. And of course one could continue to use generics. But further thought showed that the implementation burden was not so great after all and nobody understood the tagged type technique which was really incredibly contorted. Moreover, the continued use of generics when other languages forty years ago had included a more natural mechanism was tiresome. So at long last Ada 2005 includes anonymous access to subprogram types.

We rewrite the integration function much as follows

function Integrate(
         Fn: access function (X: Float) return Float;
         Lo, Hi: Float) return Float is
   Total: Float;
   N: constant Integer := ... ;    -- no of subdivisions
   Step: Float := (Hi – Lo) / Float(N);
   X: Float := Lo;     -- current point
begin
   Total := 0.5 * Fn(Lo);    -- value at low bound
   for I in 1 .. N–1 loop
      X := X + Step;    -- add values at
      Total := Total + Fn(X);    -- intermediate points
   end loop;
   Total := Total + 0.5 * Fn(Hi);    -- add final value
   return Total * Step;    -- normalize
end Integrate;

The important thing to notice is the profile of Integrate in which the parameter Fn is of an anonymous access to subprogram type. We have also shown a simple body which uses the trapezium/trapezoid method and so calls the actual function corresponding to Fn at the two end points of the range and at a number of equally spaced intermediate points.

(NB It is time for a linguistic interlude. Roughly speaking English English trapezium equals US English trapezoid. They both originate from the Greek τραπεζα meaning a table (literally with four feet). Both originally meant a quadrilateral with no pairs of sides parallel. In the late 17th century, trapezium came to mean having one pair of sides parallel. In the 18th century trapezoid came to mean the same as trapezium but promptly faded out of use in England whereas in the US it continues in use. Meanwhile in the US, trapezium reverted to its original meaning of totally irregular. Trapezoid is rarely used in the UK but if used has reverted to its original meaning of totally irregular. A standard language would be useful. Anyway, the integration is using quadrilateral strips with one pair of sides parallel.)

With this new declaration of Integrate, the accessibility problems are overcome and we are allowed to write Integrate(F'Access, ... ) just as we could write P(X'Access) in the example in the previous section where we discussed anonymous access to object types.

We still have to consider how a type conversion which would permit an assignment to a global variable is prevented. The following text illustrates both access to object and access to subprogram parameters.

procedure P(
              Objptr: access Integer;
              Procptr: access procedure (X: in out Float)) is
begin
   Evil_Obj := AOT(Objptr);    -- fails at run time
   Evil_Proc := APT(Procptr);    -- fails at compile time
end P;

declare
   An_Obj: aliased Integer;
   procedure A_Proc(X: in out Float) is
   begin ... end A_Proc;
begin
   P(An_Obj'Access, A_Proc'Access);    -- legal
end;

This repeats some of the structure of the previous section. The procedure P has an access to object parameter Objptr and an access to subprogram parameter Procptr; they are both of anonymous type. The call of P in the local block passes the addresses of a local object An_Obj and a local procedure A_Proc to P. This is permitted. We now attempt to assign the parameter values from within P to global objects Evil_Obj and Evil_Proc with the intent of assigning indirectly via Evil_Obj and calling indirectly via Evil_Proc after the object and procedure referred to no longer exist.

Both of these wicked deeds are prevented by the accessibility rules.

In the case of the object parameter Objptr it knows the accessibility level of the actual An_Obj and this is seen to be greater than that of the type AOT and so the conversion is prevented at run time and in fact Program_Error is raised. But if An_Obj had been declared at the same level as AOT and not within an inner block then the conversion would have been permitted.

However, somewhat different rules apply to anonymous access to subprogram parameters. They do not carry an indication of the accessibility level of the actual parameter but simply treat it as if it were infinite (strictly – deeper than anything else). This of course prevents the conversion to the type APT and all is well; this is detected at compile time. But note that if the procedure A_Proc had been declared at the same level as APT then the conversion would still have failed because the accessibility level is treated as infinite.

There are a number of reasons for the different treatment of anonymous access to subprogram types. A big problem is that named access to subprogram types are implemented in the same way as C *func in almost all compilers. Permitting the conversion from anonymous access to subprogram types to named ones would thus have caused problems because that model does not work especially for display based implementations. Carrying the accessibility level around would not have prevented these conversions. The key goal was simply to provide a facility corresponding to that in Pascal and not to encourage too much fooling about with access to subprogram types. Recall that the attribute Unchecked_Access is permitted for access to object types but was considered far too dangerous for access to subprogram types for similar reasons.

The reader may be feeling both tired and that there are other ways around the problems of accessibility anyway. Thus the double integration presented in the Introduction can easily be circumvented in many cases. We computed

using the following program

with Integrate;
procedure Main is
   function G(X: Float) return Float is
      function F(Y: Float) return Float is
      begin
         return X*Y;
      end F;
   begin
      return Integrate(F'Access, 0.0, 1.0);
   end G;

The essence of the problem was that F had to be declared inside G because it needed access to the parameter X of G. But the astute reader will note that this example is not very convincing because the integrals can be separated and the functions both declared at library level thus

and so it all works using the Ada 95 version of Integrate anyway.

However, if the two integrals had been more convoluted or perhaps the region had not been square but triangular so that the bound of the inner integral depended on the outer variable as in

then nested functions would be vital.

We will now consider a more elegant example which illustrates how we might integrate an arbitrary function of two variables F(x, y) over a rectangular region.

Assume that we have the function Integrate for one dimension as before

function Integrate(
          Fn: access function(X: Float) return Float;
          LoX, HiX: Float;
          LoY, HiY: Float) return Float is
   function FnX(X: Float) return Float is
      function FnY(Y: Float) return Float is
      begin
         return Fn(X, Y);
      end FnY;
   begin
      return Integrate(FnY'Access, LoY, HiY);
   end FnX;
begin
   return Integrate(FnX'Access, LoX, HiX);
end integrate;

The new function Integrate for two dimensions overloads and uses the function Integrate for one dimension (a good example of overloading). With this generality it is again impossible to arrange the structure in a manner which is legal in Ada 95.

We might use the two-dimensional integration routine to solve the original trivial problem as follows

As an exercise the reader might like to rewrite the two dimensional function to work on a non-rectangular domain. The trick is to pass the bounds of the inner integral also as functions. The profile then becomes

function Integrate(
        Fn: access function (X, Y: Float) return Float;
        LoX, HiX: Float;
        LoY, HiY: access function(X: Float) return Float)
                                        return Float;

In case the reader should think that this topic is all too mathematical it should be pointed out that anonymous access to subprogram parameters are widely used in the new container library thereby saving the unnecessary use of generics.

For example the package Ada.Containers.Vectors declares procedures such as

This updates the element of the vector Container whose index is Index by calling the procedure Process with that element as parameter. Thus if we have a vector of integers V and we need to double the value of those with index in the range 5 to 10, then we would first declare a procedure such as

Further details of the use of access to subprogram types with containers will be found in a later chapter (see 8.2).

Finally it should be noted that anonymous access to subprogram types can also be used in all those places where anonymous access to object types are allowed. That is as stand-alone objects, as components of arrays and records, as function results, in renamings, and in access discriminants.

The reader who likes long sequences of reserved words should realise by now that there is no limit in Ada 2005. This is because a function without parameters can return an access to function as its result and this in turn could be of a similar kind. So we would have

Rationale for Ada 2005

3.4 Downward closures